 研究文献发布相关信息

论文题目：Composition design of a novel Ti-6Mo-3.5Cr-1Zr alloy with high-strength and ultrahigh-ductility

发表时间：Available online 29 May 2022

发表期刊： Journal of Materials Science & Technology [ 点击下载PDF ]

 研究文献内容展示

The Ti-6Mo-3.5Cr-1Zr (wt.%) was designed based on the concept of multi-effect coupling. Fig. 1 displays the M_d - B_o map based on the D-electrons theory, in which various zones with distinct plastic deformation mechanisms are divided by transition lines, such as β/ β+ ω , β+ ω / β_tw , Martensite start ( M_s ), Martensite finish ( M_f ), Martensite stress-induced ( M_d ), and α+ β/ β lines. By adjusting the relative content of the three alloying elements Mo, Cr, and Zr, the position of the alloy composition in this work corresponds to the overlap between the twinning, ω phase transformation, and dislocation slip zones. Therefore, the alloy was expected to exhibit both high strength and ε_f through the combination of the TRIP, TWIP, and dislocation strengthening effects during the plastic deformation process.

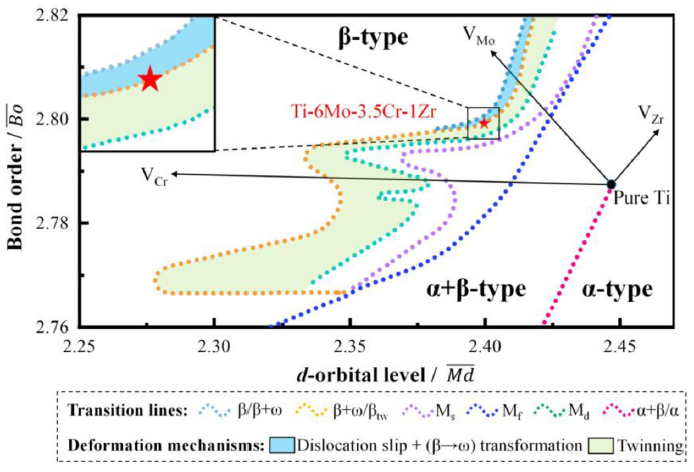
Fig. 1. D -electrons design map showing the position of the Ti-6Mo-3.5Cr-1Zr alloy.

The EBSD maps of the in-situ tension experiment are illustrated in Fig. 4 . We paused the tensile test when doing the data collection. However, it might be noted that the specimen was not removed from the in-situ stretching instrument, so as to ensure that the stress would not be unloaded. The yield strain and yield strength of the specimen are between 1.25%–1.5% and 680–700 MPa respectively according to the in-situ true stress–strain curve ( Fig. 4 (a)), which are consistent with the ex-situ curves. The alloy shows no obvious microstructural changes during the elastic deformation stage and still consists of equiaxed βgrains ( Figs. 4 (b, c) and S1 in the Supplementary Material). However, during the plastic deformation stage, a band structure is formed and its volume fraction increased with the accumulation of strain ( Figs. 4 (d, e) and S1). According to the phase map, the band structures are determined as the hexagonal structure ( Fig. 4 (f)). EBSD and TEM characterizations (see Section 3.4 for details) were combined to identify this type of band structure as the SI_ω phase. The orientation relationship between the SI_ω and the β matrix is （1-101）_SIω//（110）_β（Fig.4(g)). Prior to the rotation of the β matrix, the grains of the SI_ω phase start to rotate at low strain and their texture along the tensile direction change from (01-10) to (-12-10) and (0001) ( Fig. 4 (h)). For comparison, the texture of the βphase remains relatively unchanged ( Fig. 4 (i)).

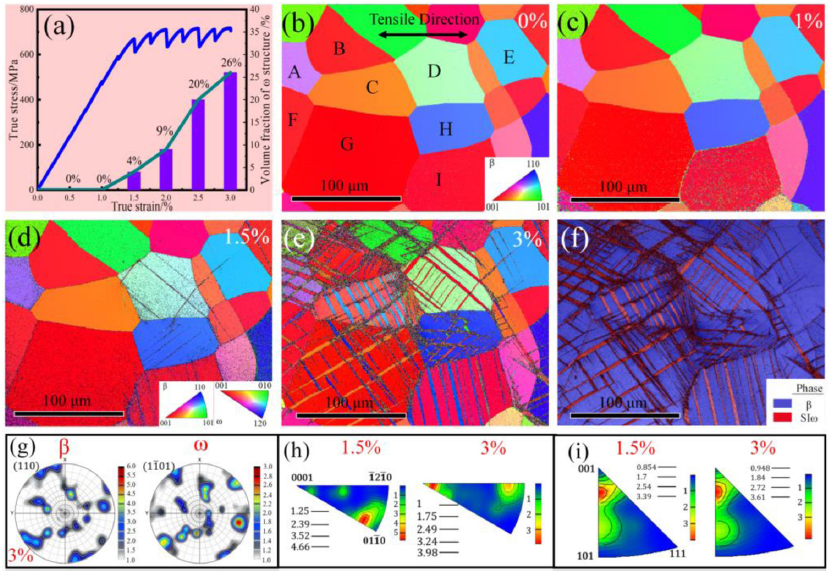
Fig. 4. In-situ EBSD analysis of the alloy at 0%–3% strain. (a) True stress–strain curve of the in-situ tensile test and the variation of the stress-induced ω volume fraction with different macro strains. (b–e) Orientation distribution maps at 0%, 1%, 1.5%, and 3% strains, respectively. (f) Phase map at 3% strain. (g) Pole Figure (PF) comparison of (110)_β and (1-101)_SIω at 3% strain. (h, i) Inverse Pole Figure (IPF) comparison between the 1.5% and 3% strains for the ω and βphases, respectively.

After comparing the IPF map ( Fig. 6 (a)) and the phase map ( Fig. 6 (b)) under 5% strain, a part of the bands in grain A is revealed as BCC structures. The boundary misorientation between the βmatrix and these bands is determined to be ∼50.5° from the inset in Fig. 6 (a), which is the boundary characteristic of {332} <113> β_tw. Additionally, secondary bands are discovered in the primary bands ( Fig. 6 (c)). The density of the geometrically necessary dislocation (GND) near the SIω zone is significantly higher than that in the β_tw and β matrix zones ( Fig. 6 (d)), which indicated that the SIω zone had an obstructive effect on the movement of dislocations. At a 10% strain state, the stress-induced bands interact with each other, forming a net-like distribution ( Fig. 6 (e, f)). Interestingly, the volume fraction of these bands further increased compared to the 5% strain state. A large number of secondary bands are precipitated in almost all primary bands ( Fig. 6 (g)). Furthermore, the average GND density at this state reaches 1.22 ×10¹⁵ m^-2 , which is higher than that at 5% strain (0.56 ×10¹⁵ m^-2 ) ( Fig. 6 (h)). As a result, the interaction of secondary deformation mechanisms and the boundaries of primary bands attributes to the increased strain hardening.

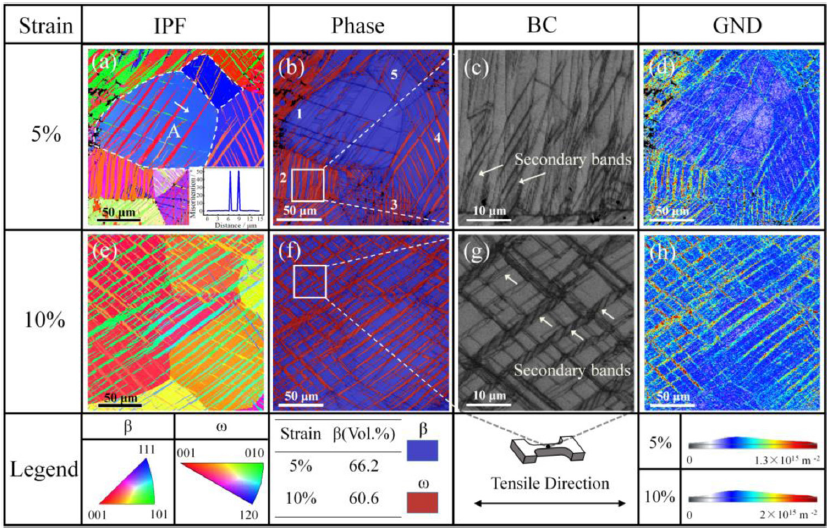
Fig. 6. Ex-situ EBSD analysis of the alloy at 5% and 10% macro strains. (a) and (e) IPF maps. (b) and (f) Phase maps. (c) and (g) BC maps. (d) and (h) GND maps.

The finer nano-scale microstructural evolution was explored by the TEM analysis. Fig. 7 (a) shows the initial formation of the SIω band at 1.5% strain. Its selected area electron diffraction (SAED) spots are discovered to coincide with those of the athermal ω₁ variant that pre-existed in the matrix ( Fig. 7 (b)). The TEM darkfield (DF) images of the ω₁ and ω₂ variants reveal that the band interior contains more ω₁ variants than the matrix, but no ω₂ variants are detected inside the band ( Fig. 7 (c, d)). Therefore, it is speculated that the precipitation of the SIω band at the initial stage of plastic deformation demonstrated a variant preference, which was believed to be related to the nucleation and growth of the ω₁ variant and the degradation of the ω₂ variant. The bent band under 2.5% strain is determined as the ω phase ( Fig. 7 (e, f)). The deformed areas in the band verify that the newly generated SIω phase actively participates in the plastic deformation ( Fig. 7 (g)).

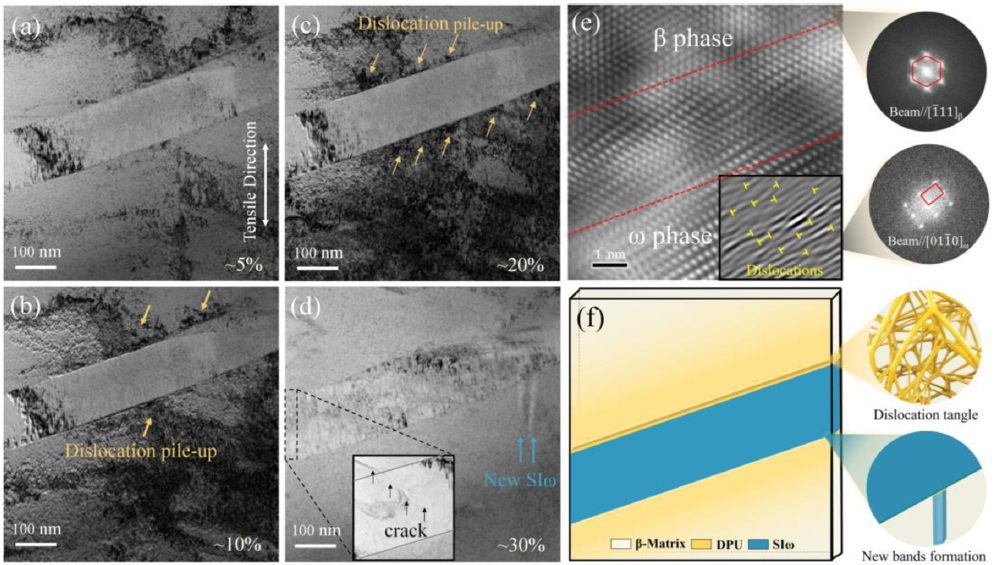
Fig. 7. TEM analysis of the tensile samples at different strains: (a–d) 1.5%. (e–g) 2.5%. (a, e) TEM bright-field (BF) images. (b, f) SAED pattern recorded from the red circle marked zone in (a) and (e), respectively. (c, d) DF images of the ω₁ and ω₂ variants based on the reflections in (b), corresponding to the dotted frame zone in (a). (g) DF image corresponding to (e).